It is time to modernise the way players are valued. Their contribution to the team’s performance should take into account the importance of the game given the margin of victory. I examine the recent Alexander Cup victory by Kingston
John Foley
This was the most successful season in our history. At our recent annual general meeting, the number of games played by each player was praised. Each person’s contribution over the season makes a difference. Traditionally there have been prizes awarded for the best performance over the season. At Kingston, we have trophy dedicated for that purpose – the elusive Silver Queen. However, this year we did not award the prize or pore over the game statistics, which was a welcome relief. Instead, we paid tribute to the effort made by our players. There were no defaults – we managed to get a full team out each match. This season we had 60 matches, double that of last season. Each match is a challenge in terms of assembling the team and travel logistics, quite apart from fretting about the chess itself.
We can reflect on what went well. Most of all, credit goes to the players. According to our club survey, most of our members are seeking to improve their chess. This is why we try to give each member as many games as possible. Even a draw can make a difference in a tight match. We want our players not only to perform well, but also to have a fighting spirit. No accepting draws to save some Elo points, but instead strive for a team victory. Several matches turned on just one game. If only there were a way to place a precise value on each player’s results, taking into account the importance of their game towards the overall result. Fortunately, there is a rigorous way of doing this – the Shapley value of a game.
Lloyd Shapley was a game theorist who won the Nobel Prize for Economics in 2012. His big idea was to find a way to unravel the contributions made by each member of a team towards a result. This problem could happen in many diverse contexts, for example sharing the cost of a taxi after a chess match where people travel home to different destinations, or indeed the cost of a celebratory meal.

To illustrate the Shapley concept, consider the relative contribution made by members of our victorious Alexander Cup team, captained by Ljubica Lazarevic. We got a bye in the first round and won all three matches from the quarter-final. To keep things simple, I include only the five players who played in each round. Others made sterling contributions – one person winning both the two games they played – but we cannot evaluate their contribution to a match in which they did not participate.
To keep personalities out of this, I shall call the players Albert, Bill, Colin, Dylan and Ethan, A, B, C, D, E. Their results were as follows:
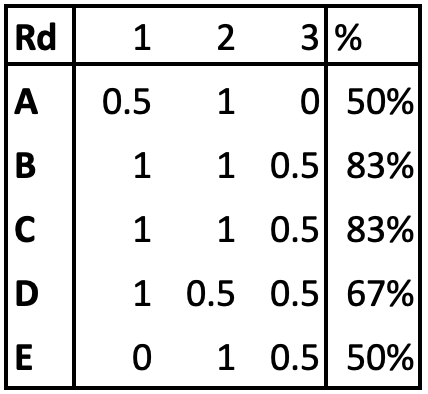
The traditional way of valuing contributions is to conclude that players B and C performed best because they got the best percentage results. There are two issues with such a inference. Firstly, the higher the board, the stronger the opponent. Of course, this is also a problem with the traditional method. A mitigating factor is that the players are in strength order so, at least in well-matched teams, the ratings of the opposing players are correlated. A more practical consideration is that we want to keep our assessments amenable to simple calculations. If we wanted to be precise, and take into account the expected likelihood of winning based upon Elo ratings, then our calculations would become unwieldy. The second issue is that securing a result in a tight match is more important than winning a game in a match in which one team thrashes the other – the winning point is diluted. This is where we can use the Shapley approach.
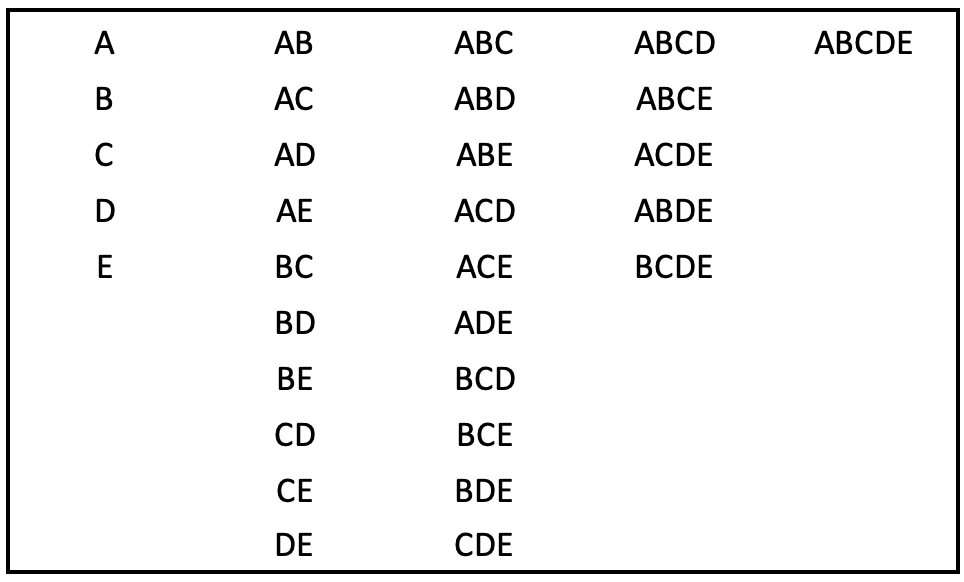
We start by considering all the possible combinations of the results of the players. With five players, there are 31 different combinations comprising five single results, 10 pairs, 10 triples, 5 quadruples and one quintuple. In each case, the test is if that combination of players’ results would have secured a victory. If you want to perform a similar calculation yourself, the combination listing for five players is set out at the foot of the column.
Against each combination you indicate whether it would have won the match. The results of the other five “irregular” players remain the same – they are not being evaluated. If a match could have been won, then all the players named in that combination are given a score of 1, otherwise zero. A drawn match can be ignored in the context of a knockout cup – we are only interest in results which contribute to a victory.
Having carried out the calculations, the rankings are as follows:
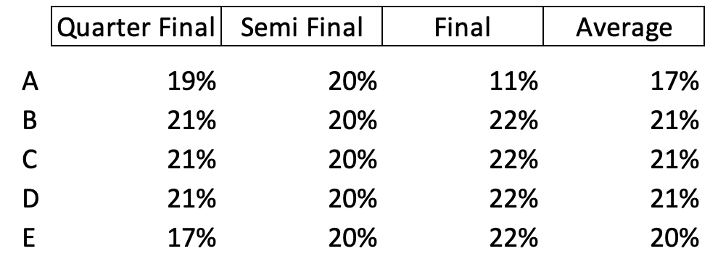
This shows quite a different picture from the traditional format. Perhaps the most notable difference is in relation to player D, who has been ranked equally with players B and C. This can be explained by what happened in the semi-final when player D only scored a draw and players B and C won their games. Our “irregular” players had racked up three points out of five games so that the five regular players needed to score 2.5 points. In fact, they won four games and drew one. Under this scenario, any combination involving results from only one or two players would be insufficient. However, if we look at combinations of three games, then whether we score 2.5 or 3 Kingston achieves victory. Hence, the contribution of Player B is worth the same as for players B and C. We can recognise D as equally deserving praise.
Another aspect of the Shapley approach is that it is a fairer description of the relative contribution of each player. On the traditional approach, B and C are given all the plaudits. However, under systematic scrutiny we can see that the contribution of all the players is much closer: each player contributes around one-fifth to the success of the team, with relatively small differences, which places three players at 21%, with the other two players being slightly below 20%. This is surely more reflective of how the team members and captain felt about their relative contributions.
Shapley values are different from Elo ratings. Both depend upon performance, but Shapley takes into account the state of the match, whereas Elo ratings only take into account the two players concerned. Shapley is about co-operative teams, whereas Elo is about competing individuals.
Chess should start to rank team players according to game theory. Each chess league, as a service to their constituent clubs, could publish the Shapley rankings for each of the players. Other sports can follow. This is what happened with Elo ratings, which other sports such as football adopted after several decades.

Combination table for five players